Robust Bayesian Model-Averaged Meta-Regression

František Bartoš

2024-12-12

Robust Bayesian model-averaged meta-regression (RoBMA-reg) extends the robust Bayesian model-averaged meta-analysis (RoBMA) by including covariates in the meta-analytic model. RoBMA-reg allows for estimating and testing the moderating effects of study-level covariates on the meta-analytic effect in a unified framework (e.g., accounting for uncertainty in the presence vs. absence of the effect, heterogeneity, and publication bias). This vignette illustrates how to fit a robust Bayesian model-averaged meta-regression using the RoBMA R package. We reproduce the example from Bartoš, Maier, Stanley, et al. (2023), who re-analyzed a meta-analysis of the effect of household chaos on child executive functions with the mean age and assessment type covariates based on Andrews et al. (2021)’s meta-analysis.

First, we fit a frequentist meta-regression using the metafor R package. Second, we explain the Bayesian meta-regression model specification, the default prior distributions for continuous and categorical moderators, and standardized effect sizes input specification. Third, we estimate Bayesian model-averaged meta-regression (without publication bias adjustment). Finally, we estimate the complete robust Bayesian model-averaged meta-regression.

Data

We start by loading the Andrews2021 dataset included in the RoBMA R package, which contains 36 estimates of the effect of household chaos on child executive functions with the mean age and assessment type covariates. The dataset includes correlation coefficients (r), standard errors of the correlation coefficients (se), the type of executive function assessment (measure), and the mean age of the children (age) in each study.

library(RoBMA)
data("Andrews2021", package = "RoBMA")
head(Andrews2021)
#>       r         se measure      age
#> 1 0.070 0.04743416  direct 4.606660
#> 2 0.033 0.04371499  direct 2.480833
#> 3 0.170 0.10583005  direct 7.750000
#> 4 0.208 0.08661986  direct 4.000000
#> 5 0.270 0.02641969  direct 4.000000
#> 6 0.170 0.05147815  direct 4.487500

Frequentist Meta-Regression

We start by fitting a frequentist meta-regression using the metafor R package (Wolfgang, 2010). While Andrews et al. (2021) estimated univariate meta-regressions for each moderator, we directly proceed by analyzing both moderators simultaneously. For consistency with original reporting, we estimate the meta-regression using the correlation coefficients and the standard errors provided by (Andrews et al., 2021); however, note that Fisher’s z transformation is recommended for estimating meta-analytic models (e.g., Stanley et al. (2024)).

fit_rma <- metafor::rma(yi = r, sei = se, mods = ~ measure + age, data = Andrews2021)
fit_rma
#> 
#> Mixed-Effects Model (k = 36; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of residual heterogeneity):     0.0150 (SE = 0.0045)
#> tau (square root of estimated tau^2 value):             0.1226
#> I^2 (residual heterogeneity / unaccounted variability): 91.28%
#> H^2 (unaccounted variability / sampling variability):   11.47
#> R^2 (amount of heterogeneity accounted for):            15.24%
#> 
#> Test for Residual Heterogeneity:
#> QE(df = 33) = 340.7613, p-val < .0001
#> 
#> Test of Moderators (coefficients 2:3):
#> QM(df = 2) = 7.5445, p-val = 0.0230
#> 
#> Model Results:
#> 
#>                   estimate      se    zval    pval    ci.lb   ci.ub     
#> intrcpt             0.0898  0.0467  1.9232  0.0545  -0.0017  0.1813   . 
#> measureinformant    0.1202  0.0466  2.5806  0.0099   0.0289  0.2115  ** 
#> age                 0.0030  0.0062  0.4867  0.6265  -0.0091  0.0151     
#> 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The results reveal a statistically significant moderation effect of the executive function assessment type on the effect of household chaos on child executive functions ($p = 0.0099$). To explore the moderation effect further, we estimate the estimated marginal means for the executive function assessment type using the emmeans R package (Lenth et al., 2017).

emmeans::emmeans(metafor::emmprep(fit_rma), specs = "measure")
#>  measure   emmean     SE  df asymp.LCL asymp.UCL
#>  direct     0.109 0.0305 Inf    0.0492     0.169
#>  informant  0.229 0.0347 Inf    0.1612     0.297
#> 
#> Confidence level used: 0.95

Studies using the informant-completed questionnaires show a stronger effect of household chaos on child executive functions, r = 0.229, 95% CI [0.161, 0.297], than the direct assessment, r = 0.109, 95% CI [0.049, 0.169]; both types of studies show statistically significant effects.

The mean age of the children does not significantly moderate the effect ($p = 0.627$) with the estimated regression coefficient of b = 0.003, 95% CI [-0.009, 0.015]. As usual, frequentist inference limits us to failing to reject the null hypothesis. Here, we try to overcome this limitation with Bayesian model-averaged meta-regression.

Bayesian Meta-Regression Specification

Before we proceed with the Bayesian model-averaged meta-regression, we provide a quick overview of the regression model specification. In contrast to frequentist meta-regression, we need to specify prior distributions on the regression coefficients, which encode the tested hypotheses about the presence vs. absence of the moderation (specifying different prior distributions corresponds to different hypotheses and results in different conclusions). Importantly, the treatment of continuous and categorical covariates differs in the Bayesian model-averaged meta-regression.

Continuous vs. Categorical Moderators and Default Prior Distributions

The default prior distribution for continuous moderators is a normal prior distribution with mean of 0 and a standard deviation of 1/4. In other words, the default prior distribution assumes that the effect of the moderator is small and smaller moderation effects are more likely than larger effects. The default choice for continuous moderators can be overridden by the prior_covariates argument (for all continuous covariates) or by the priors argument (for specific covariates, see ?RoBMA.reg for more information). The package automatically standardizes the continuous moderators. This achieves scale-invariance of the specified prior distributions and ensures that the prior distribution for the intercept correspond to the grand mean effect. This setting can be overridden by specifying the standardize_predictors = FALSE argument.

The default prior distribution for the categorical moderators is a normal distribution with a mean of 0 and a standard deviation of 1/4, representing the deviation of each level from the grand mean effect. The package uses standardized orthonormal contrasts (contrast = "meandif") to model deviations of each category from the grand mean effect. The default choice for categorical moderators can be overridden by the prior_factors argument (for all categorical covariates) or by the priors argument (for specific covariates, see ?RoBMA.reg for more information). The "meandif" contrasts achieve label invariance (i.e., the coding of the categorical covariates does not affect the results) and the prior distribution for the intercept corresponds to the grand mean effect. Alternatively, the package also allows specifying "treatment" contrasts, which result in a prior distribution on the difference between the default level and the remaining levels of the categorical covariate (with the intercept corresponding to the effect in the default factor level).

Effect Size Input Specification

Prior distributions for Bayesian meta-analyses are calibrated for the standardized effect size measures. As such, the fitting function needs to know what kind of effect size was supplied as the input. In RoBMA() function, this is achieved by the d, r, logOR, OR, z, se, v, n, lCI, and uCI arguments. The input is passed to the combine_data() function in the background that combines the effect sizes and merges them into a single data.frame. The RoBMA.reg() (and NoBMA.reg()) function requires the dataset to be passed as a data.frame (without missing values) with column names identifying the - moderators passed using the formula interface (i.e., ~ measure + age in our example) - and the effect sizes and standard errors (i.e., r and se in our example).

As such, it is crucial for the column names to correctly identify the standardized effect sizes, standard errors, sample sizes, and moderators.

Bayesian Model-Averaged Meta-Regression

We fit the Bayesian model-averaged meta-regression using the NoBMA.reg() function (the NoBMA.reg() function is a wrapper around the RoBMA.reg() function that automatically removes models adjusting for publication bias). We specify the model formula with the ~ operator similarly to the rma() function and pass the dataset as a data.frame with named columns as outlined in the section above (the names need to identify the moderators and effect size measures). We also set the parallel = TRUE argument to speed up the computation by running the chains in parallel and seed = 1 argument to ensure reproducibility.

fit_BMA <- NoBMA.reg(~ measure + age, data = Andrews2021, parallel = TRUE, seed = 1)

Note that the NoBMA.reg() function specifies the combination of all models assuming presence vs. absence of the effect, heterogeneity, moderation by measure, and moderation by age, which corresponds to $2*2*2*2=16$ models. Including each additional moderator doubles the number of models, leading to an exponential increase in model count and significantly longer fitting times.

Once the ensemble is estimated, we can use the summary() functions with the output_scale = "r" argument, which produces meta-analytic estimates that are transformed to the correlation scale.

summary(fit_BMA, output_scale = "r")
#> Call:
#> RoBMA.reg(formula = formula, data = data, test_predictors = test_predictors, 
#>     study_names = study_names, study_ids = study_ids, transformation = transformation, 
#>     prior_scale = prior_scale, standardize_predictors = standardize_predictors, 
#>     effect_direction = "positive", priors = priors, model_type = model_type, 
#>     priors_effect = priors_effect, priors_heterogeneity = priors_heterogeneity, 
#>     priors_bias = NULL, priors_effect_null = priors_effect_null, 
#>     priors_heterogeneity_null = priors_heterogeneity_null, priors_bias_null = prior_none(), 
#>     priors_hierarchical = priors_hierarchical, priors_hierarchical_null = priors_hierarchical_null, 
#>     prior_covariates = prior_covariates, prior_covariates_null = prior_covariates_null, 
#>     prior_factors = prior_factors, prior_factors_null = prior_factors_null, 
#>     chains = chains, sample = sample, burnin = burnin, adapt = adapt, 
#>     thin = thin, parallel = parallel, autofit = autofit, autofit_control = autofit_control, 
#>     convergence_checks = convergence_checks, save = save, seed = seed, 
#>     silent = silent)
#> 
#> Bayesian model-averaged meta-regression (normal-normal model)
#> Components summary:
#>               Models Prior prob. Post. prob. Inclusion BF
#> Effect          8/16       0.500       1.000 6.637645e+05
#> Heterogeneity   8/16       0.500       1.000 3.439130e+40
#> 
#> Meta-regression components summary:
#>         Models Prior prob. Post. prob. Inclusion BF
#> measure   8/16       0.500       0.826        4.739
#> age       8/16       0.500       0.197        0.245
#> 
#> Model-averaged estimates:
#>      Mean Median 0.025 0.975
#> mu  0.163  0.163 0.118 0.208
#> tau 0.121  0.120 0.086 0.167
#> The effect size estimates are summarized on the correlation scale and heterogeneity is summarized on the Fisher's z scale (priors were specified on the Cohen's d scale).
#> 
#> Model-averaged meta-regression estimates:
#>                            Mean Median  0.025 0.975
#> intercept                 0.163  0.163  0.118 0.208
#> measure [dif: direct]    -0.047 -0.051 -0.099 0.000
#> measure [dif: informant]  0.047  0.051  0.000 0.099
#> age                       0.003  0.000 -0.011 0.043
#> The effect size estimates are summarized on the correlation scale and heterogeneity is summarized on the Fisher's z scale (priors were specified on the Cohen's d scale).

The summary function produces output with multiple sections The first section contains the Components summary with the hypothesis test results for the overall effect size and heterogeneity. We find overwhelming evidence for both with inclusion Bayes factors (Inclusion BF) above 10,000.

The second section contains the Meta-regression components summary with the hypothesis test results for the moderators. We find moderate evidence for the moderation by the executive function assessment type, $\text{BF}_{\text{measure}} = 4.74$. Furthermore, we find moderate evidence for the null hypothesis of no moderation by mean age of the children, $\text{BF}_{\text{age}} = 0.245$ (i.e., BF for the null is $1/0.245 = 4.08$). These findings extend the frequentist meta-regression by disentangling the absence of evidence from the evidence of absence.

The third section contains the Model-averaged estimates with the model-averaged estimates for mean effect $\rho = 0.16$, 95% CI [0.12, 0.21] and between-study heterogeneity $\tau_{\text{Fisher's z}} = 0.12$, 95% CI [0.09, 0.17].

The fourth section contains the Model-averaged meta-regression estimates with the model-averaged regression coefficient estimates. The main difference from the usual frequentist meta-regression output is that the categorical predictors are summarized as a difference from the grand mean for each factor level. Here, the intercept regression coefficient estimate corresponds to the grand mean effect and the measure [dif: direct] regression coefficient estimate of -0.047, 95% CI [-0.099, 0.000] corresponds to the difference between the direct assessment and the grand mean. As such, the results suggest that the effect size in studies using direct assessment is lower in comparison to the grand mean of the studies. The age regression coefficient estimate is standardized, therefore, the increase of 0.003, 95% CI [-0.011, 0.043] corresponds to the increase in the mean effect when increasing mean age of children by one standard deviation.

Similarly to the frequentist meta-regression, we can use the marginal_summary() function to obtain the marginal estimates for each of the factor levels.

marginal_summary(fit_BMA, output_scale = "r")
#> Call:
#> RoBMA.reg(formula = formula, data = data, test_predictors = test_predictors, 
#>     study_names = study_names, study_ids = study_ids, transformation = transformation, 
#>     prior_scale = prior_scale, standardize_predictors = standardize_predictors, 
#>     effect_direction = "positive", priors = priors, model_type = model_type, 
#>     priors_effect = priors_effect, priors_heterogeneity = priors_heterogeneity, 
#>     priors_bias = NULL, priors_effect_null = priors_effect_null, 
#>     priors_heterogeneity_null = priors_heterogeneity_null, priors_bias_null = prior_none(), 
#>     priors_hierarchical = priors_hierarchical, priors_hierarchical_null = priors_hierarchical_null, 
#>     prior_covariates = prior_covariates, prior_covariates_null = prior_covariates_null, 
#>     prior_factors = prior_factors, prior_factors_null = prior_factors_null, 
#>     chains = chains, sample = sample, burnin = burnin, adapt = adapt, 
#>     thin = thin, parallel = parallel, autofit = autofit, autofit_control = autofit_control, 
#>     convergence_checks = convergence_checks, save = save, seed = seed, 
#>     silent = silent)
#> 
#> Robust Bayesian meta-analysis
#> Model-averaged marginal estimates:
#>                     Mean Median 0.025 0.975 Inclusion BF
#> intercept          0.163  0.163 0.118 0.208          Inf
#> measure[direct]    0.117  0.116 0.052 0.185       50.151
#> measure[informant] 0.208  0.210 0.130 0.280          Inf
#> age[-1SD]          0.160  0.161 0.106 0.208          Inf
#> age[0SD]           0.163  0.163 0.118 0.208          Inf
#> age[1SD]           0.166  0.165 0.117 0.220          Inf
#> The estimates are summarized on the correlation scale (priors were specified on the Cohen's d scale).
#> mu_intercept: Posterior samples do not span both sides of the null hypothesis. The Savage-Dickey density ratio is likely to be overestimated.
#> mu_measure[informant]: Posterior samples do not span both sides of the null hypothesis. The Savage-Dickey density ratio is likely to be overestimated.
#> mu_age[-1SD]: Posterior samples do not span both sides of the null hypothesis. The Savage-Dickey density ratio is likely to be overestimated.
#> mu_age[0SD]: There is a considerable cluster of prior samples at the exact null hypothesis values. The Savage-Dickey density ratio is likely to be invalid.
#> mu_age[0SD]: Posterior samples do not span both sides of the null hypothesis. The Savage-Dickey density ratio is likely to be overestimated.
#> mu_age[1SD]: Posterior samples do not span both sides of the null hypothesis. The Savage-Dickey density ratio is likely to be overestimated.

The estimated marginal means are similar to the frequentist results. Studies using the informant-completed questionnaires again show a stronger effect of household chaos on child executive functions, $\rho = 0.208$, 95% CI [0.130, 0.280], than the direct assessment, $\rho = 0.117$, 95% CI [0.052, 0.185].

The last column summarizes results from a test against a null hypothesis of marginal means equals 0. Here, we find very strong evidence for the effect size of studies using the informant-completed questionnaires differing from zero, $\text{BF}_{10} = 50.1$ and extreme evidence for the effect size of studies using the direct assessment differing from zero, $\text{BF}_{10} = \infty$. The test is performed using the change from prior to posterior distribution at 0 (i.e., the Savage-Dickey density ratio) assuming the presence of the overall effect or the presence of difference according to the tested factor. Because the tests use prior and posterior samples, calculating the Bayes factor can be problematic when the posterior distribution is far from the tested value. In such cases, warning messages are printed and $\text{BF}_{10} = \infty$ returned (like here)—while the actual Bayes factor is less than infinity, it is still too large to be computed precisely given the posterior samples.

The full model-averaged posterior marginal means distribution can be visualized by the marginal_plot() function.

marginal_plot(fit_BMA, parameter = "measure", output_scale = "r", lwd = 2)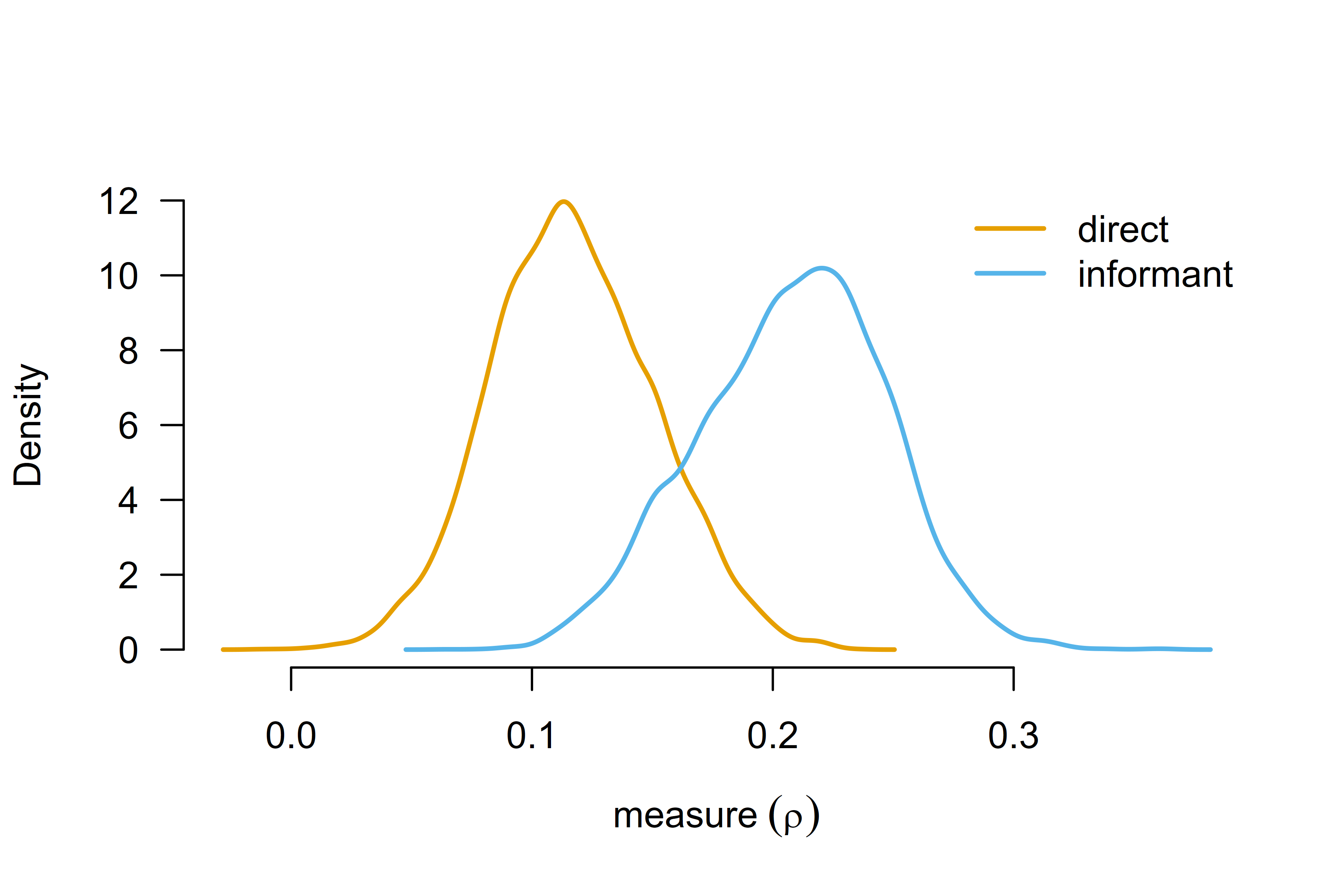

Robust Bayesian Model-Averaged Meta-Regression

Finally, we adjust the Bayesian model-averaged meta-regression model by fitting the robust Bayesian model-averaged meta-regression. In contrast to the previous publication bias unadjusted model ensemble, RoBMA-reg extends the model ensemble by the publication bias component specified via 6 weight functions and PET-PEESE (Bartoš, Maier, Wagenmakers, et al., 2023). We use the RoBMA.reg() function with the same arguments as in the previous section. The estimation time further increases as the ensemble now contains 144 models.

fit_RoBMA <- RoBMA.reg(~ measure + age, data = Andrews2021, parallel = TRUE, seed = 1)

summary(fit_RoBMA, output_scale = "r")
#> Call:
#> RoBMA.reg(formula = ~measure + age, data = Andrews2021, chains = 1, 
#>     parallel = TRUE, seed = 1)
#> 
#> Robust Bayesian meta-regression
#> Components summary:
#>                Models Prior prob. Post. prob. Inclusion BF
#> Effect         72/144       0.500       0.334 5.020000e-01
#> Heterogeneity  72/144       0.500       1.000 1.043816e+23
#> Bias          128/144       0.500       0.965 2.795800e+01
#> 
#> Meta-regression components summary:
#>         Models Prior prob. Post. prob. Inclusion BF
#> measure 72/144       0.500       0.950       19.086
#> age     72/144       0.500       0.154        0.182
#> 
#> Model-averaged estimates:
#>                    Mean Median 0.025  0.975
#> mu                0.031  0.000 0.000  0.164
#> tau               0.106  0.104 0.074  0.147
#> omega[0,0.025]    1.000  1.000 1.000  1.000
#> omega[0.025,0.05] 0.999  1.000 1.000  1.000
#> omega[0.05,0.5]   0.998  1.000 1.000  1.000
#> omega[0.5,0.95]   0.997  1.000 1.000  1.000
#> omega[0.95,0.975] 0.997  1.000 1.000  1.000
#> omega[0.975,1]    0.997  1.000 1.000  1.000
#> PET               2.056  2.494 0.000  3.293
#> PEESE             1.916  0.000 0.000 19.068
#> The effect size estimates are summarized on the correlation scale and heterogeneity is summarized on the Fisher's z scale (priors were specified on the Cohen's d scale).
#> (Estimated publication weights omega correspond to one-sided p-values.)
#> 
#> Model-averaged meta-regression estimates:
#>                            Mean Median  0.025 0.975
#> intercept                 0.031  0.000  0.000 0.164
#> measure [dif: direct]    -0.063 -0.064 -0.106 0.000
#> measure [dif: informant]  0.063  0.064  0.000 0.106
#> age                       0.000  0.000 -0.024 0.022
#> The effect size estimates are summarized on the correlation scale and heterogeneity is summarized on the Fisher's z scale (priors were specified on the Cohen's d scale).

All previously described functions for manipulating the fitted model work identically with the publication bias adjusted model. As such, we just briefly mention the main differences found after adjusting for publication bias.

RoBMA-reg reveals strong evidence of publication bias $\text{BF}_{\text{pb}} = 28.0$. Furthermore, accounting for publication bias turns the previously found evidence for the overall effect into a weak evidence against the effect $\text{BF}_{10} = 0.50$ and notably reduces the mean effect estimate $\rho = 0.031$, 95% CI [0.000, 0.164].

marginal_summary(fit_RoBMA, output_scale = "r")
#> Call:
#> RoBMA.reg(formula = ~measure + age, data = Andrews2021, chains = 1, 
#>     parallel = TRUE, seed = 1)
#> 
#> Robust Bayesian meta-analysis
#> Model-averaged marginal estimates:
#>                      Mean Median  0.025 0.975 Inclusion BF
#> intercept           0.031  0.000  0.000 0.164        0.516
#> measure[direct]    -0.031 -0.056 -0.105 0.121        0.575
#> measure[informant]  0.093  0.077  0.000 0.223        7.643
#> age[-1SD]           0.031  0.000 -0.015 0.163        0.732
#> age[0SD]            0.031  0.000  0.000 0.164        1.013
#> age[1SD]            0.031  0.000 -0.024 0.168        0.743
#> The estimates are summarized on the correlation scale (priors were specified on the Cohen's d scale).
#> mu_age[0SD]: There is a considerable cluster of prior samples at the exact null hypothesis values. The Savage-Dickey density ratio is likely to be invalid.

The estimated marginal means now suggest that studies using the informant-completed questionnaires show a much smaller effect of household chaos on child executive functions, $\rho = 0.093$, 95% CI [0.000, 0.223] with only moderate evidence against no effect, $\text{BF}_{10} = 7.64$, while studies using direct assessment even provide weak evidence against the effect of household chaos on child executive functions, $\text{BF}_{10} = 0.58$, with most likely effect sizes around zero, $\rho = -0.031$, 95% CI [-0.105, 0.121].

A visual summary of the estimated marginal means highlights the considerably wider model-averaged posterior distributions of the marginal means—a consequence of accounting and adjusting for publication bias.

marginal_plot(fit_RoBMA, parameter = "measure", output_scale = "r", lwd = 2)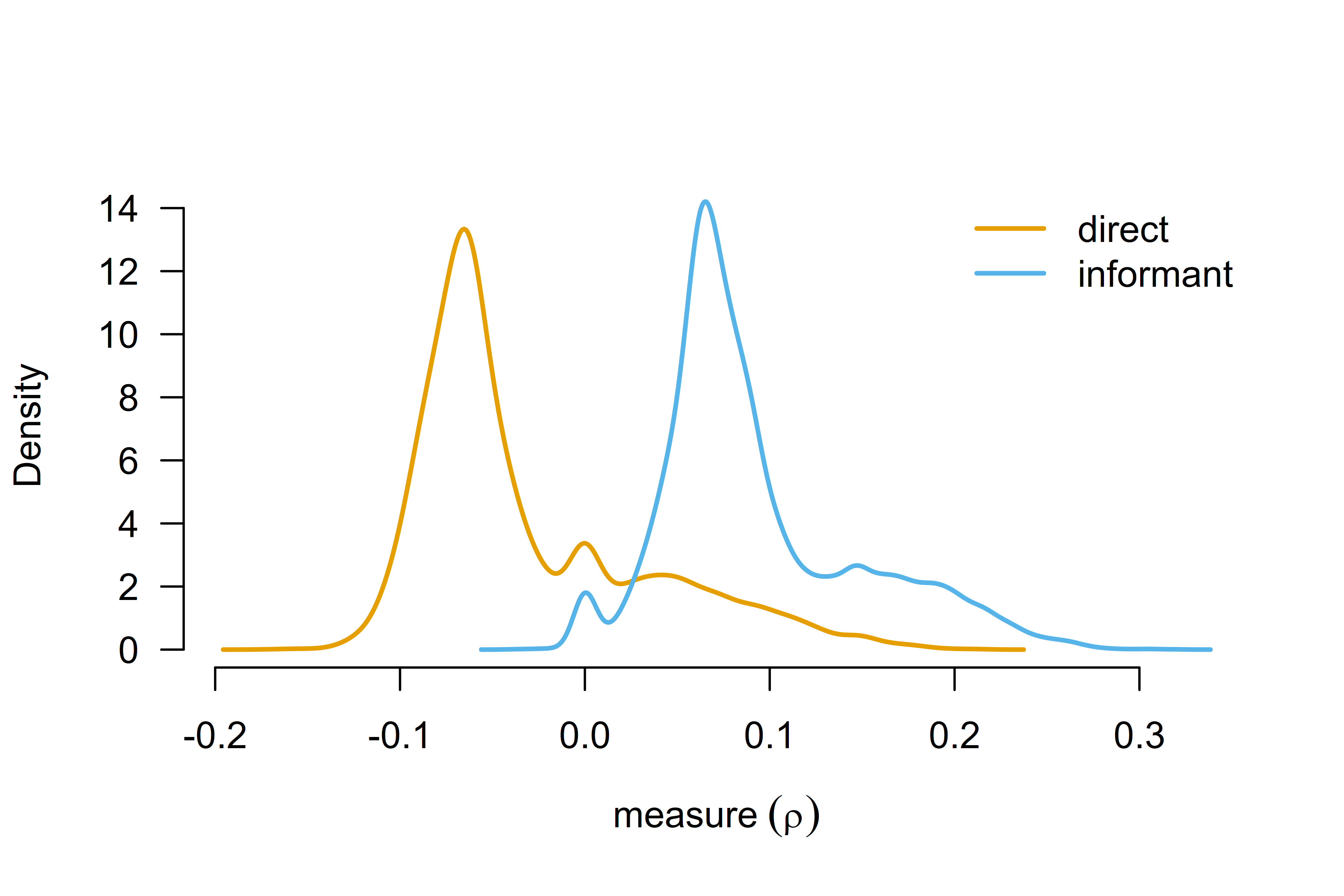

The Bayesian model-averaged meta-regression models are compatible with the remaining custom specification, visualization, and summary functions included in the RoBMA R package, highlighted in other vignettes. E.g., custom model specification is demonstrated in the vignette Fitting Custom Meta-Analytic Ensembles and visualizations and summaries are demonstrated in the Reproducing BMA and Informed Bayesian Model-Averaged Meta-Analysis in Medicine vignettes.

References

Andrews, K., Atkinson, L., Harris, M., & Gonzalez, A. (2021). Examining the effects of household chaos on child executive functions: A meta-analysis. Psychological Bulletin, 147(1), 16–32. https://doi.org/10.1037/bul0000311

Bartoš, F., Maier, M., Stanley, T., & Wagenmakers, E.-J. (2023). Robust Bayesian meta-regression—Model-averaged moderation analysis in the presence of publication bias. https://doi.org/10.31234/osf.io/98xb5

Bartoš, F., Maier, M., Wagenmakers, E.-J., Doucouliagos, H., & Stanley, T. D. (2023). Robust Bayesian meta-analysis: Model-averaging across complementary publication bias adjustment methods. Research Synthesis Methods, 14(1), 99–116. https://doi.org/10.1002/jrsm.1594

Lenth, R. V., Bolker, B., Buerkner, P., Giné-Vázquez, I., Herve, M., Jung, M., Love, J., Miguez, F., Riebl, H., & Singmann, H. (2017). emmeans: Estimated marginal means, aka least-squares means. https://cran.r-project.org/package=emmeans

Stanley, T., Doucouliagos, H., Maier, M., & Bartoš, F. (2024). Correcting bias in the meta-analysis of correlations. Psychological Methods. https://doi.org/10.1037/met0000662

Wolfgang, V. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://www.jstatsoft.org/v36/i03/