Hierarchical Bayesian Model-Averaged Meta-Analysis

František Bartoš

2024-12-12

Hierarchical (or multilevel/3-level) meta-analysis adjusts for the dependency of effect sizes due to clustering in the data. For example, effect size estimates from multiple experiments reported in the same manuscript might be expected to be more similar than effect sizes from a different paper (Konstantopoulos, 2011). This vignette illustrates how to deal with such dependencies among effect size estimates (in cases with simple nested structure) using the Bayesian model-averaged meta-analysis (BMA) (Bartoš et al., 2021; Gronau et al., 2017, 2021). (See other vignettes for more details on BMA: Reproducing BMA or Informed BMA in medicine.)

First, we introduce the example data set. Second, we illustrate the frequentist hierarchical meta-analysis with the metafor R package and discuss the results. Third, we outline the hierarchical meta-analysis parameterization. Fourth, we estimate the Bayesian model-averaged hierarchical meta-analysis. Finally, we conclude by discussing further extensions and publication bias adjustment.

Example Data Set

We use the dat.konstantopoulos2011 data set from the metadat R package (Thomas et al., 2019) that is used for the same functionality in the metafor (Wolfgang, 2010) R package. We roughly follow the example in the data set’s help file, ?dat.konstantopoulos2011. The data set consists of 56 studies estimating the effects of modified school calendars on students’ achievement. The 56 studies were run in individual schools, which can be grouped into 11 districts. We might expect more similar effect size estimates from schools in the same district – in other words, the effect size estimates from the same district might not be completely independent. Consequently, we might want to adjust for this dependency (clustering) between the effect size estimates to draw a more appropriate inference.

First, we load the data set, assign it to the dat object, and inspect the first few rows.

data("dat.konstantopoulos2011", package = "metadat")
dat <- dat.konstantopoulos2011

head(dat)
#>   district school study year    yi    vi
#> 1       11      1     1 1976 -0.18 0.118
#> 2       11      2     2 1976 -0.22 0.118
#> 3       11      3     3 1976  0.23 0.144
#> 4       11      4     4 1976 -0.30 0.144
#> 5       12      1     5 1989  0.13 0.014
#> 6       12      2     6 1989 -0.26 0.014

In the following analyses, we use the following variables:

• yi, standardized mean differences,
• vi, sampling variances of the standardized mean differences,
• district, district id which distinguishes among the districts,
• and school, that distinguishes among different schools within the same district.

Frequentist Hierarchical Meta-Analysis with metafor

We follow the data set’s help file and fit a simple random effects meta-analysis using the rma() function from metafor package. This model ignores the dependency between effect size estimates. We use this simple model as our starting point and as a comparison with the later models.

fit_metafor.0 <- metafor::rma(yi = yi, vi = vi, data = dat)
fit_metafor.0
#> 
#> Random-Effects Model (k = 56; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of total heterogeneity): 0.0884 (SE = 0.0202)
#> tau (square root of estimated tau^2 value):      0.2974
#> I^2 (total heterogeneity / total variability):   94.70%
#> H^2 (total variability / sampling variability):  18.89
#> 
#> Test for Heterogeneity:
#> Q(df = 55) = 578.8640, p-val < .0001
#> 
#> Model Results:
#> 
#> estimate      se    zval    pval   ci.lb   ci.ub     
#>   0.1279  0.0439  2.9161  0.0035  0.0419  0.2139  ** 
#> 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The model summary returns a small but statistically significant effect size estimate $\mu = 0.128$ ($\text{se} = 0.044$) and a considerable heterogeneity estimate $\tau = 0.297$.

We extend the model to account for the hierarchical structure of the data, i.e., schools within districts, by using the rma.mv() function from the metafor package and extending it with the random = ~ school | district argument.

fit_metafor <- metafor::rma.mv(yi, vi, random = ~ school | district, data = dat)
fit_metafor
#> 
#> Multivariate Meta-Analysis Model (k = 56; method: REML)
#> 
#> Variance Components:
#> 
#> outer factor: district (nlvls = 11)
#> inner factor: school   (nlvls = 11)
#> 
#>             estim    sqrt  fixed 
#> tau^2      0.0978  0.3127     no 
#> rho        0.6653             no 
#> 
#> Test for Heterogeneity:
#> Q(df = 55) = 578.8640, p-val < .0001
#> 
#> Model Results:
#> 
#> estimate      se    zval    pval   ci.lb   ci.ub    
#>   0.1847  0.0846  2.1845  0.0289  0.0190  0.3504  * 
#> 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We find that accounting for the hierarchical structure of the data results in (1) a slightly larger effect size estimate ($\mu = 0.187$) and (2) larger standard error of the effect size estimate ($\text{se} = 0.085$). The larger standard error is a natural consequence of accounting for the dependency between the effect sizes. Because the effect sizes are dependent, they contribute less additional information than independent effect sizes would. Specifying the hierarchical model then accounts for the dependency by estimating similarity between the estimates from the same cluster (school) and discounting the information borrowed from each estimate. The estimate of the similarity among estimates from the same cluster is summarized in the \rho = 0.666 estimate.

Specifications of Hierarchical Meta-Analysis

We specify a simple hierarchical meta-analytic model (see Konstantopoulos (2011) for an example). Using distributional notation, we can describe the data generating process as a multi-stage sampling procedure. In a nutshell, we assume the existence of an overall mean effect $\mu$. Next, we assume that the effect sizes in each district $k = 1, \dots, K$, $\gamma_k$, systematically differ from the mean effect, with the variance of the district-level effects summarized with heterogeneity $\tau_{b}$ (as between). Furthermore, we assume that the true effects $\theta_{k,j}$ of each study $j = 1, \dots J_k$ systematically differ from the district-level effect, with the variance of the study effects from the district-level effect summarized with heterogeneity $\tau_{w}$ (as within). Finally, the observed effect sizes $y_{k,j}$ that differ from the true effects $y_{k,j}$ due to random errors $\text{se}_{k,j}$.

Mathematically, we can describe such a model as: $$\begin{aligned} \gamma_k &\sim \text{N}(\mu, \tau_b^2),\\ \theta_{k,j} &\sim \text{N}(\gamma_k, \tau_w^2),\\ y_{k,j} &\sim \text{N}(\theta_{k,j}, \text{se}_{k,j}).\\ \end{aligned}$$ Where N() denotes a normal distribution with mean and variance.

Conveniently, and with a bit of algebra, we do not need to estimate the district-level and true study effects. Instead, we marginalize them out, and we sample the observed effect sizes from each district $y_{k,.}$ directly from a multivariate normal distributions, MN(), with a common mean $\mu$ and covariance matrix S: $$\begin{aligned} y_{k,.} &\sim \text{MN}(\mu, \text{S}),\\ \text{S} &= \begin{bmatrix} \tau_b^2 + \tau_w^2 + \text{se}_1^2 & \tau_w^2 & \dots & \tau_w^2 \\ \tau_w^2 & \tau_b^2 + \tau_w^2 + \text{se}_2^2 & \dots & \tau_w^2 \\ \dots & \dots & \dots & \dots \\ \tau_w^2 & \tau_w^2 & \dots & \tau_b^2 + \tau_w^2 + \text{se}_{J_k}^2 & \\ \end{bmatrix}. \end{aligned}$$ The random effects marginalization is helpful as it allows us to sample fewer parameters from the posterior distribution (which significantly simplifies marginal likelihood estimation via bridge sampling). Furthermore, the marginalization allows us to properly specify selection model publication bias adjustment models – the marginalization propagates the selection process up through all the sampling steps at once (we cannot proceed with the sequential sampling as the selection procedure on the observed effect sizes modifies the sampling distributions of all the preceding levels).

We can further re-parameterize the model by performing the following substitution, $$\begin{aligned} \tau^2 &= \tau_b^2 + \tau_w^2,\\ \rho &= \frac{\tau_w^2}{\tau_b^2 + \tau_w^2}, \end{aligned}$$ and specifying the covariance matrix using the inter-study correlation $\rho$, total heterogeneity $\tau$, and the standard errors $\text{se}_{.}$: $$\begin{aligned} \text{S} &= \begin{bmatrix} \tau^2 + \text{se}_1^2 & \rho\tau^2 & \dots & \rho\tau^2 \\ \rho\tau^2 & \tau^2 + \text{se}_2^2 & \dots & \rho\tau^2 \\ \dots & \dots & \dots & \dots \\ \rho\tau^2 & \rho\tau^2 & \dots & \tau^2 + \text{se}_{J_k}^2 & \\ \end{bmatrix}. \end{aligned}$$ This specification corresponds to the compound symmetry covariance matrix of random effects, the default settings in the metafor::rma.mv() function. More importantly, it allows us to easily specify prior distributions on the correlation coefficient $\rho$ and the total heterogeneity $\tau$.

Hierarchical Bayesian Model-Averaged Meta-Analysis with RoBMA

Before we estimate the complete Hierarchical Bayesian Model-Averaged Meta-Analysis (hBMA) with the RoBMA package, we briefly reproduce the simpler models we estimated with the metafor package in the previous section.

Bayesian Random Effects Meta-Analysis

First, we estimate a simple Bayesian random effects meta-analysis (corresponding to fit_metafor.0). We use the RoBMA() function and specify the effect sizes and sampling variances via the d = dat$yi and v = dat$vi arguments. We set the priors_effect_null, priors_heterogeneity_null, and priors_bias arguments to null to omit models assuming the absence of the effect, heterogeneity, and the publication bias adjustment components.

fit.0 <- RoBMA(d = dat$yi, v = dat$vi,
               priors_effect_null        = NULL,
               priors_heterogeneity_null = NULL,
               priors_bias               = NULL,
               parallel = TRUE, seed = 1)

We generate a complete summary for the only estimated model by adding the type = "individual" argument to the summary() function.

summary(fit.0, type = "individual")
#> Call:
#> RoBMA(d = dat$yi, v = dat$vi, priors_bias = NULL, priors_effect_null = NULL, 
#>     priors_heterogeneity_null = NULL, parallel = TRUE, seed = 1)
#> 
#> Robust Bayesian meta-analysis                                                               
#>  Model              1             Parameter prior distributions
#>  Prior prob.    1.000                    mu ~ Normal(0, 1)     
#>  log(marglik)   17.67                   tau ~ InvGamma(1, 0.15)
#>  Post. prob.    1.000                                          
#>  Inclusion BF     Inf                                          
#> 
#> Parameter estimates:
#>      Mean    SD   lCI Median   uCI error(MCMC) error(MCMC)/SD  ESS R-hat
#> mu  0.126 0.043 0.041  0.127 0.211     0.00044          0.010 9757 1.000
#> tau 0.292 0.033 0.233  0.290 0.364     0.00034          0.010 9678 1.000
#> The estimates are summarized on the Cohen's d scale (priors were specified on the Cohen's d scale).

We verify that the effect size, $\mu = 0.126$ ($\text{95$), and heterogeneity, $\tau = 0.292$ ($\text{95$), estimates closely correspond to the frequentist results (as we would expect from parameter estimates under weakly informative priors).

Hierarchical Bayesian Random Effects Meta-Analysis

Second, we account for the clustered effect size estimates within districts by extending the previous function call with the study_ids = dat$district argument. This allows us to estimate the hierarchical Bayesian random effects meta-analysis (corresponding to fit_metafor). We use the default prior distribution for the correlation parameter \rho \sim \text{Beta}(1, 1), set via the priors_hierarchical argument, which restricts the correlation to be positive and uniformly distributed on the interval $(0, 1)$.

fit <- RoBMA(d = dat$yi, v = dat$vi, study_ids = dat$district,
             priors_effect_null        = NULL,
             priors_heterogeneity_null = NULL,
             priors_bias               = NULL,
             parallel = TRUE, seed = 1)

Again, we generate the complete summary for the only estimated model,

summary(fit, type = "individual")
#> Call:
#> RoBMA(d = dat$yi, v = dat$vi, study_ids = dat$district, priors_bias = NULL, 
#>     priors_effect_null = NULL, priors_heterogeneity_null = NULL, 
#>     parallel = TRUE, seed = 1)
#> 
#> Robust Bayesian meta-analysis                                                               
#>  Model              1             Parameter prior distributions
#>  Prior prob.    1.000                    mu ~ Normal(0, 1)     
#>  log(marglik)   25.70                   tau ~ InvGamma(1, 0.15)
#>  Post. prob.    1.000                   rho ~ Beta(1, 1)       
#>  Inclusion BF     Inf                                          
#> 
#> Parameter estimates:
#>      Mean    SD   lCI Median   uCI error(MCMC) error(MCMC)/SD  ESS R-hat
#> mu  0.181 0.083 0.017  0.180 0.346     0.00088          0.011 9041 1.000
#> tau 0.308 0.056 0.223  0.299 0.442     0.00090          0.016 3859 1.000
#> rho 0.627 0.142 0.320  0.641 0.864     0.00219          0.015 4202 1.000
#> The estimates are summarized on the Cohen's d scale (priors were specified on the Cohen's d scale).

and verify that our estimates, again, correspond to the frequentist counterparts, with the estimated effect size, $\mu = 0.181$ ($\text{95$), heterogeneity, $\tau = 0.308$ ($\text{95$), and correlation, $\rho = 0.627$ ($\text{95$).

We can further visualize the prior and posterior distribution of the $\rho$ parameter using the plot() function.

par(mar = c(2, 4, 0, 0))
plot(fit, parameter = "rho", prior = TRUE)

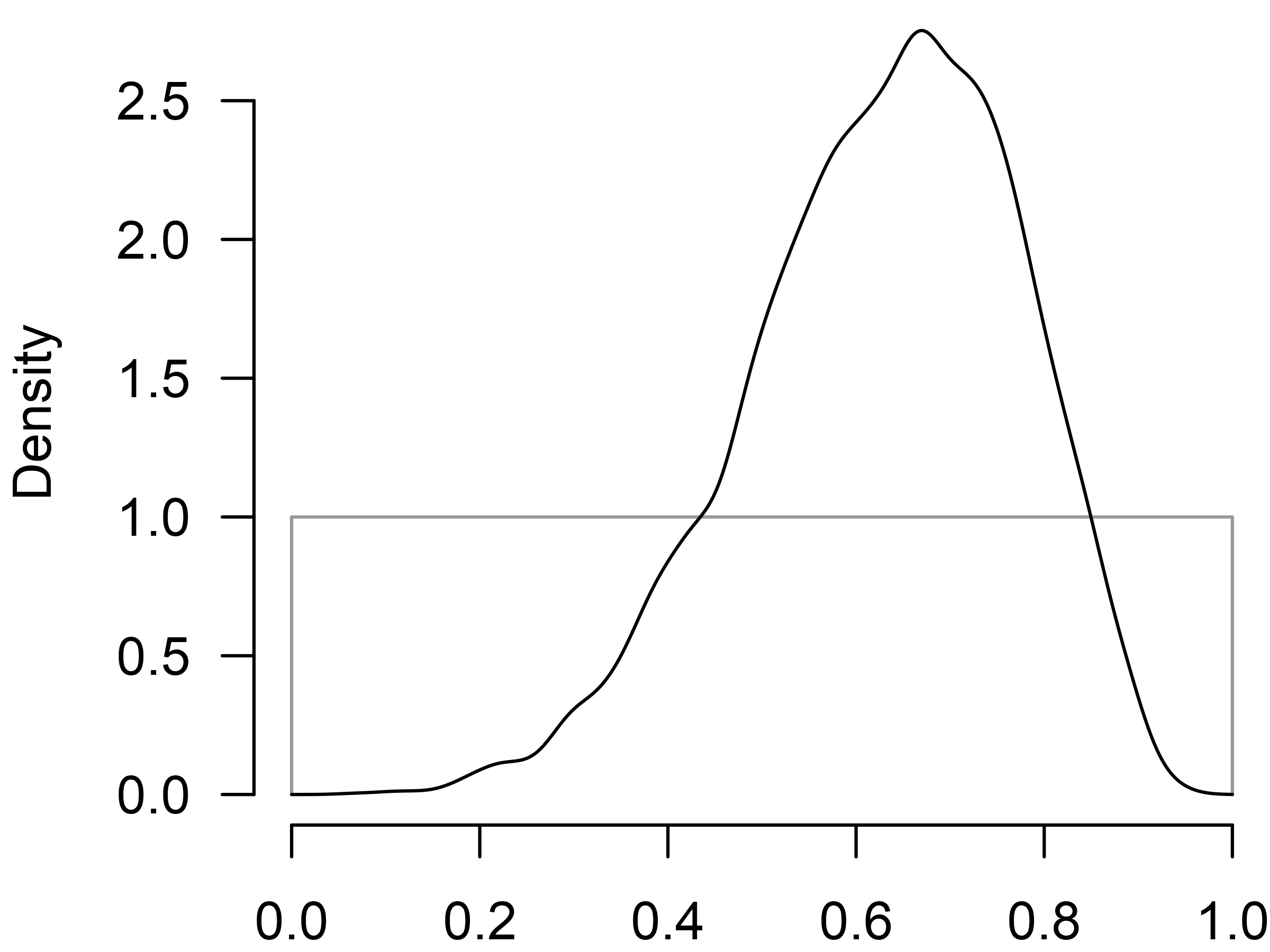
Hierarchical Bayesian Model-Averaged Meta-Analysis

Third, we extend the previous model into a model ensemble that also includes models assuming the absence of the effect and/or heterogeneity (we do not incorporate models assuming presence of publication bias due to computational complexity explained in the summary). Including those additional models allows us to evaluate evidence in favor of the effect and heterogeneity. Furthermore, specifying all those additional models allows us to incorporate the uncertainty about the specified models and weight the posterior distribution according to how well the models predicted the data. We estimate the remaining models by removing the priors_effect_null and priors_heterogeneity_null arguments from the previous function calls, which include the previously omitted models of no effect and/or no heterogeneity.

fit_BMA <- RoBMA(d = dat$yi, v = dat$vi, study_ids = dat$district,
                 priors_bias = NULL,
                 parallel = TRUE, seed = 1)

Now we generate a summary for the complete model-averaged ensemble by not specifying any additional arguments in the summary() function.

summary(fit_BMA)
#> Call:
#> RoBMA(d = dat$yi, v = dat$vi, study_ids = dat$district, priors_bias = NULL, 
#>     parallel = TRUE, seed = 1)
#> 
#> Robust Bayesian meta-analysis
#> Components summary:
#>               Models Prior prob. Post. prob. Inclusion BF
#> Effect           2/4       0.500       0.478 9.170000e-01
#> Heterogeneity    2/4       0.500       1.000 9.326943e+92
#> Hierarchical     2/4       0.500       1.000 9.326943e+92
#> 
#> Model-averaged estimates:
#>      Mean Median 0.025 0.975
#> mu  0.087  0.000 0.000 0.314
#> tau 0.326  0.317 0.231 0.472
#> rho 0.659  0.675 0.354 0.879
#> The estimates are summarized on the Cohen's d scale (priors were specified on the Cohen's d scale).

We find the ensemble contains four models, the combination of models assuming the presence/absence of the effect/heterogeneity, each with equal prior model probabilities. Importantly, the models assuming heterogeneity are also specified with the hierarchical structure and account for the clustering. A comparison of the specified models reveals weak evidence against the effect, $\text{BF}_{10} = 0.917$, and extreme evidence for the presence of heterogeneity, $\text{BF}_{\text{rf}} = 9.3\times10^{92}$. Moreover, we find that the Hierarchical component summary has the same values as the Heterogeneity component summary because the default settings specify that all models assuming the presence of heterogeneity also include the hierarchical structure.

We also obtain the model-averaged posterior estimates that combine the posterior estimates from all models according to the posterior model probabilities, the effect size, $\mu = 0.087$ ($\text{95$), heterogeneity, $\tau = 0.326$ ($\text{95$), and correlation, $\rho = 0.659$ ($\text{95$).

Testing the Presence of Clustering

In the previous analyses, we assumed that the effect sizes are indeed clustered within the districts, and we only adjusted for the clustering. However, the effect sizes within the same cluster may not be more similar than effect sizes from different clusters. Now, we specify a model ensemble that allows us to test this assumption by specifying two sets of random effect meta-analytic models. The first set of models assumes that there is indeed clustering and that the correlation of random effects is uniformly distributed on the $(0, 1)$ interval (as in the previous analyses). The second set of models assumes that there is no clustering, i.e., the correlation of random effects $\rho = 0$, which simplifies the structured covariance matrix to a diagonal matrix. Again, we model average across models assuming the presence and absence of the effect to account for the model uncertainty.

To specify this ‘special’ model ensemble with the RoBMA() function, we need to modify the previous model call in the following ways. We removed the fixed effect models by specifying the priors_heterogeneity_null = NULL argument.$^1$ Furthermore, we specify the prior distribution for models assuming the absence of the hierarchical structure by adding the priors_hierarchical_null = prior(distribution = "spike", parameters = list("location" = 0)) argument.

hierarchical_test <- RoBMA(d = dat$yi, v = dat$vi, study_ids = dat$district,
                           priors_heterogeneity_null = NULL,
                           priors_hierarchical_null = prior(distribution = "spike", parameters = list("location" = 0)),
                           priors_bias = NULL,
                           parallel = TRUE, seed = 1)

summary(hierarchical_test)
#> Call:
#> RoBMA(d = dat$yi, v = dat$vi, study_ids = dat$district, priors_bias = NULL, 
#>     priors_heterogeneity_null = NULL, priors_hierarchical_null = prior(distribution = "spike", 
#>         parameters = list(location = 0)), parallel = TRUE, seed = 1)
#> 
#> Robust Bayesian meta-analysis
#> Components summary:
#>               Models Prior prob. Post. prob. Inclusion BF
#> Effect           2/4       0.500       0.478        0.917
#> Heterogeneity    4/4       1.000       1.000          Inf
#> Hierarchical     2/4       0.500       1.000     4624.794
#> 
#> Model-averaged estimates:
#>      Mean Median 0.025 0.975
#> mu  0.087  0.000 0.000 0.314
#> tau 0.326  0.317 0.231 0.472
#> rho 0.659  0.675 0.354 0.879
#> The estimates are summarized on the Cohen's d scale (priors were specified on the Cohen's d scale).

We summarize the resulting model ensemble and find out that the Hierarchical component is no longer equivalent to the Heterogeneity component – the new model specification allowed us to compare random effect models assuming the presence of the hierarchical structure to random effect models assuming the absence of the hierarchical structure. The resulting inclusion Bayes factor of the hierarchical structure shows extreme evidence in favor of clustering of the effect sizes, $\text{BF}_{\rho\bar{\rho}} = 4624$, i.e., there is extreme evidence that the intervention results in more similar effects within the districts.

Summary

We illustrated how to estimate a hierarchical Bayesian model-averaged meta-analysis using the RoBMA package. The hBMA model allows us to test for the presence vs absence of the effect and heterogeneity while simultaneously adjusting for clustered effect size estimates. While the current implementation allows us to draw a fully Bayesian inference, incorporate prior information, and acknowledge model uncertainty, it has a few limitations in contrast to the metafor package. E.g., the RoBMA package only allows a simple nested random effects (i.e., estimates within studies, schools within districts etc). The simple nesting allows us to break the full covariance matrix into per cluster block matrices which speeds up the already demanding computation. Furthermore, the computational complexity significantly increases when considering selection models as we need to compute an exponentially increasing number of multivariate normal probabilities with the increasing cluster size (existence of clusters with more than four studies makes the current implementation impractical due to the computational demands). However, these current limitations are not the end of the road, as we are exploring other approaches (e.g., only specifying PET-PEESE style publication bias adjustment and other dependency adjustments) in a future vignette.

Footnotes

$^1$ We could also model-average across the hierarchical structure assuming fixed effect models, i.e., $\tau \sim f(.)$ and $\rho = 1$. However specifying such a model ensemble is a beyond the scope of this vignette, see Custom ensembles vignette for some hints.

References

Bartoš, F., Gronau, Q. F., Timmers, B., Otte, W. M., Ly, A., & Wagenmakers, E.-J. (2021). Bayesian model-averaged meta-analysis in medicine. Statistics in Medicine, 40(30), 6743–6761. https://doi.org/10.1002/sim.9170

Gronau, Q. F., Heck, D. W., Berkhout, S. W., Haaf, J. M., & Wagenmakers, E.-J. (2021). A primer on Bayesian model-averaged meta-analysis. Advances in Methods and Practices in Psychological Science, 4(3), 1–19. https://doi.org/10.1177/25152459211031256

Gronau, Q. F., Van Erp, S., Heck, D. W., Cesario, J., Jonas, K. J., & Wagenmakers, E.-J. (2017). A Bayesian model-averaged meta-analysis of the power pose effect with informed and default priors: The case of felt power. Comprehensive Results in Social Psychology, 2(1), 123–138. https://doi.org/10.1080/23743603.2017.1326760

Konstantopoulos, S. (2011). Fixed effects and variance components estimation in three-level meta-analysis. Research Synthesis Methods, 2(1), 61–76. https://doi.org/10.1002/jrsm.35⁠

Thomas, W., Daniel, N., Alistair, S., W. Kyle, H., & Wolfgang, V. (2019). metadat: Meta-analysis datasets. https://cran.r-project.org/package=metadat

Wolfgang, V. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://www.jstatsoft.org/v36/i03/